Local changes in potassium ions regulate input integration in active dendrites

To identify the expected E_K⁺ shifts under different conditions, we first undertook an analytical approach that did not include simulation of the membrane potential dynamics. We hypothesized that dendritic segments with similarly tuned inputs can attain higher [K⁺]_o changes and E_K⁺ shifts than segments with diversely tuned inputs and that this could, in turn, affect dendritic excitability (Fig 1a). To investigate this, we sampled the synaptic activity of a hypothetical 10 μm segment, populated with 7 to 13 synapses, yielding a synaptic density comparable to the neocortex [51–53]. We chose this length scale because functional clusters, comprised of inputs with similar tuning preferences, typically are formed within 5 to 10 μm [32,45–47]. To model feature-tuned synaptic inputs, we used visual orientation tuning as our framework. Previous work identified dendritic segments receiving inputs with similar or diverse orientation tuning [42,54]. To capture this, we sampled synaptic orientation preferences from a circular normal distribution for the similarly tuned regime and from a uniform distribution for the diversely tuned regime [42], and assigned tuning curves to individual synapses (Fig 1a and 1c). From the sampled segments, we obtained synapse-averaged tuning curves and activity distributions (Fig 1d and 1e). Using these, we derived an activity factor for each orientation, signifying the ratio of expected synaptic activity in segments with similar versus diverse tuning preferences (Fig 1f; see Methods). This showed that for stimulus orientations close to the target orientation, here arbitrarily chosen as the somatic preferred orientation set at 0°, (Δtarget orientation: 0–20°), synaptic activity levels are 2 to 5 times higher in segments with similarly tuned inputs than in segments with diversely tuned inputs. Contrary, for orientations far from the target orientation (Δtarget orientation: 45–90°), activity ceases almost entirely in segments with similar tuning while it remains constant for segments with diverse tuning, yielding activity factors below 1.

Fig 1. Dendritic segments with similarly tuned inputs support higher [K⁺]_o changes and E_K⁺ shifts.

(a) Diagram of the proposed hypothesis that dendritic segments with similarly tuned inputs can attain higher [K⁺]_o increases than segments with diversely tuned inputs. (b) Cumulative fraction of synapse orientation preferences relative to target orientation for dendritic segments with diverse or similar orientation tuning. Reproducing results of [42]. (c) Example dendritic segments with diverse and similar input tuning regimes (left). Synaptic tuning curves for different orientation-tuned stimuli, as per [55], normalized by the maximum activity (right). Note that the x-axis corresponds to stimulus orientation relative to target orientation. The resulting activity shows the tuning curves for the synapses indicated on the corresponding dendritic segment on the left. Based on the distributions of panel b and the synaptic tuning curves, we acquired a statistical approximation of the expected E_K⁺ shifts without explicitly modeling membrane dynamics. (d) Example synapse-averaged tuning curves for dendritic segments from the diverse (top) and similar (bottom) tuning regimes. Tuning curves of individual synapses are in gray and average is in color. (e) Probability distributions of average synaptic activity for the diverse and similar tuning regimes for the target (left) and orthogonal to the target (right) orientations. Dotted lines indicate expectation value. (f) Synaptic activity factor, defined as the ratio between expected synaptic activity for similarly—E (S) and diversely—E (D) tuned segments as a function of stimulus orientation relative to target orientation. (g) Δ[K⁺]_o as a function of stimulus orientation relative to target orientation for the diverse and similar tuning regimes. Left: different extracellular space radii (R₂) with constant [K⁺]_i reductions (Δ[K⁺]_i = 1 mM). Right: different Δ[K⁺]_i with constant R₂ (). (h) Heat maps showing the range of ΔE_K⁺ for the diverse (left) and similar (right) tuning regimes as a function of Δ[K⁺]_i and R₂ at the target orientation. Dotted lines indicate the corresponding Δ[K⁺]_o range.

https://doi.org/10.1371/journal.pbio.3002935.g001

We then asked how these synaptic activity patterns are manifested in [K⁺]_o and E_K⁺ changes. Due to experimental limitations, there is a lack of knowledge about singular ionic flux over the multiple ionic channels that support the in vitro and in vivo documented potassium concentration changes. Thus, we adopted a mean-field approach that allowed us to relate the experimental recordings of extracellular potassium to the model while keeping to the number of assumptions at a minimum. Specifically, in our approach we assumed the following conditions to be true: (1) Local increases in [K⁺]_o are proportional to synaptic activity levels; (2) local increases in [K⁺]_o are caused by K⁺ efflux from the intracellular space; and (3) [K⁺]_o change is stable in space and time along the short dendritic segment. The latter is motivated by the fact that (a) K⁺ ions in the extracellular space, of the spatial and temporal scale considered here (approximately 10 μm and approximately 300 ms after synaptic activity onset, respectively), can be described as well-mixed due to the high K⁺ free diffusion rate () [56,57]; and (b) extracellular potassium remains elevated for timescales of several hundreds of ms, as documented in in vitro experiments [58,59] (see Methods for detailed analysis). Following these assumptions, we approximated the [K⁺]_o changes of dendritic segments by multiplying the intracellular K⁺ concentration ([K⁺]_i) change by the volume fraction between the intra- and extracellular space:
(1)

Here, Δ[K⁺]_o and Δ[K⁺]_i are the changes in [K⁺]_o and [K⁺]_i, respectively. The dendritic segment is considered as a cylinder with radius R₁, encapsulated by the extracellular space, also described as a cylinder with radius R₂ (see Methods, Eq 5). By keeping the dendritic diameter constant (R₁ = 1 μm) [60,61], we limit our parameter space to 2 parameters: Δ[K⁺]_i and R₂. Although we do not have data on the local dendritic [K⁺]_i changes, nor do we know the exact extracellular space size in the vicinity of dendritic segments, we can use Eq 1 to estimate [K⁺]_o changes by varying Δ[K⁺]_i and R₂ within realistic ranges [62–64]. Note that as R₂→R₁, Δ[K⁺]_o increases as approaching infinity, and becomes undefined for R₂ = R₁. As R₂→∞, Δ[K⁺]_o goes towards zero asymptotically. By multiplying Δ[K⁺]_i for the diversely tuned input regime by the synaptic activity factor (Fig 1f), we also obtain relative estimates of [K⁺]_o changes in segments receiving similarly tuned inputs. Δ[K⁺]_o changes are positively correlated with the Δ[K⁺]_i (Fig 1g, right), inversely correlated with the size of the extracellular space (Fig 1g, left) and, for the similar input regime, higher for orientations close to the target orientation but lower for orientations far from the target (Fig 1g).

Focusing on activity for stimuli presented at Δtarget orientation = 0°, we next identified the Δ[K⁺]_i and R₂ parameters that constrained the Δ[K⁺]_o for the diversely tuned inputs to a range of 0.25–1 mM (Fig 1h, left), to reflect the changes measured by in vivo [K⁺]_o measurements using microelectrodes [5–7,9,10,12–14,18,65], a technique which averages the measured concentration in space and time and likely underestimates true local [K⁺]_o changes [66–69]. This set of parameters when applied to the similarly tuned input regime results in Δ[K⁺]_o changes in the range 1.25–5 mM (Fig 1h, right). By converting the Δ[K⁺] into shifts in E_K⁺ via the Nernst equation:
(2)
and using this parameter set, we evaluated the range of the ΔE_K⁺ shifts. For diverse inputs, the ΔE_K⁺ is within the range of 1.6–5.9 mV above the resting E_K⁺, and for similarly tuned input, the respective range is 6–18 mV (Fig 1h). Based on this analytical approach, in the following sections, we use these ranges in ΔE_K⁺ as a proxy for changes in [K⁺]_o, when we explore their impact on dendritic integration in biophysical models with different levels of abstraction. Together, these data suggest that dendritic segments receiving synaptic inputs with similar tuning preferences can attain substantially higher [K⁺]_o and E_K⁺ changes compared with segments receiving diversely tuned inputs, yet in a stimulus-specific manner.

We then investigated the implications of the identified in Fig 1 E_K⁺ shifts might have on dendritic synaptic integration. We focused on dendritic segments with similarly tuned inputs as (1) we documented stimulus orientation-dependent and large (above 15 mV) E_K⁺ shifts in these segments (Fig 1g and 1h); and (2) previous work has shown that spatial clustering of co-active inputs is an important factor for dendritic spike initiation [32–38]. For this analysis, we implemented a biophysically detailed point model to simulate the V_m of a dendritic segment during synaptic input stimulation, referred to as a “point-dendrite” model due to its similarities with a conventional point-neuron model [70] (Fig 2a; see Methods). The point-dendrite model included an array of active ion channels found in the dendrites of V1, as well as AMPA and NMDA receptors [71–73] (S1 Table). The number of synapses and their orientation tuning were sampled as in Fig 1 to simulate a dendritic segment receiving similarly tuned inputs. Synaptic inputs were activated by delivering a stimulation train consisting of 3 events in which AMPA and NMDA receptors were activated with a peak current depending on the synapse’s orientation tuning and with a Poisson-distributed delay (mean = 80 ms). This protocol induced V_m dynamics that reflected the stimulus orientation in the absence of E_K⁺ shifts (Fig 2b). Importantly, for orientations close to the target orientation, we also observed regenerative activation of NMDA conductances, leading to NMDA-dependent dendritic spikes (see Fig 3a), while for the orthogonal orientation the V_m did not change (Fig 2b) [42]. To obtain a mechanistic understanding of how E_K⁺ shifts might shape orientation tuning, we first tested their effect on dendritic spike properties (see Methods) for a stimulus presented at the target orientation, using different ΔE_K⁺ values in the predicted range of Fig 1h, ([0–18] mV). E_K⁺ shifts caused a broadening of dendritic spikes (Figs 2c, 2d and S1); for example, for a 12 mV E_K⁺ shift the duration of dendritic spikes increased by approximately 80% compared to no E_K⁺ shift. This effect persisted in the presence of nonspecific inhibitory (GABA_A) input (S2 Fig). Furthermore, the amount of excitatory synaptic drive needed to transition the dendritic V_m from subthreshold input summation to suprathreshold dendritic spiking decreased substantially with increased E_K⁺ shifts (Fig 2e and 2f).

Fig 2. E_K⁺ shifts regulate active dendritic properties.

(a) Diagram of the biophysical point-dendrite model. To test the effect of local [K⁺]_o elevations, we imposed E_K⁺ shifts within the interval of 0–18 mV. (b) Example dendrite V_m traces for the similar input tuning regime as a function of stimulus orientation relative to target orientation. Individual trials are in gray and average is in black. Shaded regions indicate synaptic stimulation timing. (c) Example V_m traces highlighting dendritic spike duration (time above –30 mV) as a function of ΔE_K⁺ at the target orientation. The E_K⁺ shift is induced following the first simulation event and is visible in the resting membrane potential of the dendritic segment. (d) Dendritic spike duration as a function of ΔE_K⁺ at the target orientation. Error bars are mean ± SEM. (N = 10 simulations). (e) Example traces highlighting V_m response as a function of ΔE_K⁺ and mean synaptic activity. (f) Heat map showing peak V_m depolarization as a function of ΔE_K⁺ and mean synaptic activity. Dotted lines indicate the transition to dendritic spiking. Number of synapses used: N = 10. (g) Dendritic spike probability as a function of ΔE_K⁺ and stimulus orientation relative to target orientation. Note that ΔE_K⁺ values denote shifts at the target orientation and shifts for the rest of the orientations are calculated using the synaptic activity factor. (h) Dendritic spike probability at the target orientation (left axis) and orientation selectivity index (right axis) as a function of ΔE_K⁺. See also S3 and S4 Figs and S1 Table.

https://doi.org/10.1371/journal.pbio.3002935.g002

In our model, 3 main parameters control dendritic spike generation: the number of dendritic synapses (N), the average synaptic activity (w), and the ΔE_K⁺ (see Methods for details). By simulating different parameter configurations with dendritic spike occurrence as binary output measure, we fitted a function that describes the minimum ΔE_K⁺ needed to trigger dendritic spiking given N and w (S3 and S4 Figs):
(3)

Using Eq (3), we estimated the probability of generating a dendritic spike for a given stimulus orientation (Fig 2g). The probability of eliciting dendritic spikes rose drastically as a function of increasing E_K⁺ shifts (Fig 2g and 2f); for example, the probability of spiking to the target orientation increased from 48% to 97% when shifting the E_K⁺ by 12 mV. This gain in the dendritic output was similar to the one expected from increasing the number of synapses (S5 Fig), with the main difference being that E_K⁺ modulation is transient, selectively boosting the activity of repetitively active dendrites. Interestingly, the dendritic spiking orientation selectivity was largely constant even though the probability of spiking increased also for orientations away from the target orientation (Fig 2g and 2h; Orientation selectivity index: 0.98, 0.98, and 0.96 for ΔE_K⁺ = 0, 6, and 18 mV, respectively). Altogether, these results show that local K⁺ changes in dendritic segments with similarly tuned synaptic inputs prolong dendritic spikes and boost the probability of generating dendritic spikes without affecting their feature selectivity.

To understand the general biophysical principles governing the regulation of dendritic spikes by local K⁺ changes, we turned to dynamical systems theory [74]. Dendritic spiking can be described by the instantaneous phase plot of the V_m and . Given that the membrane capacitance is constant, we transformed this to the I-V curve using [29]. With only the intrinsic ion channels active, V_m is attracted to a single down-stable hyperpolarized fixed point corresponding to the resting potential (Fig 3a). Inclusion of NMDA receptors changes the system to bistable, and an attractor basin together with a depolarized fixed point, corresponding to dendritic spiking, is created. The voltage barrier preventing the system from transitioning to an up-stable state, where V_m is only attracted to the depolarized fixed point, is overcome by the activation of AMPA receptors. As the activity of AMPA and NMDA receptors wears off, in conjunction with the high activity of K⁺ channels, the system is again pushed back to the down-stable state.

Fig 3. Current-voltage (I-V) relations and bistability with E_K⁺ shift.

(a) I-V curves during the generation of dendritic NMDA spike. Green: down-stable state with only intrinsic ion channels active. Blue: bistable state with intrinsic ion channels and NMDA receptor active. Red: Bi- and up-stable state with intrinsic ion channels and NMDA and AMPA receptors active. (b) Down-stable state before dendritic spike generation without and with E_K⁺ shift. Solid points indicate stable fixed points. (c, d) Bistable states during and at the end of dendritic spike without and with E_K⁺ shift. (c) Shows the hypothetical system with peak NMDA receptor conductance, without AMPA receptor activation, right before spike initiation, and (d) shows the system when outward and inward currents match for the system without E_K⁺ shift around the end of the spike. Solid and open points indicate stable and unstable fixed points, respectively. (e) Heat maps showing the temporal evolution of the I-V landscape without and with E_K⁺ shift. The corresponding I-V curves shown in (b–d) are indicated with black dotted lines, and full and dotted blue lines indicate stable and unstable fixed points, respectively. (a–c) Arrows indicate system flow direction. Note that positive inward current depolarizes the membrane, resulting in I–V plot similar to previous work (Major and colleagues [29]). See also S1 Video.

https://doi.org/10.1371/journal.pbio.3002935.g003

Shifting the E_K⁺ alters the I-V curve attractor landscape in 3 fundamental ways (Fig 3b–3e and S1 Video). First, for the down-stable state, it moves the fixed point to a more depolarized V_m, as well as reducing the net outward current across all V_m levels (Fig 3b). Second, for the bistable state, it lowers the voltage barrier needed to transition the system to the up-stable state and deepens the attractor basin (Fig 3c and 3d). Finally, by reducing the net outward currents at depolarized V_m levels, it prolongs the duration for which the system is in up- and bistable states (Fig 3c–3e). These dynamical system properties are all explained by the weakened K⁺ driving force through K⁺ channels and fully predict the ΔE_K⁺-mediated effects we observed on dendritic spiking (Fig 2). Collectively, this analysis demonstrates that the effects of local K⁺ changes on synaptic integration can be predicted by the altered dynamical system properties of dendritic spikes.

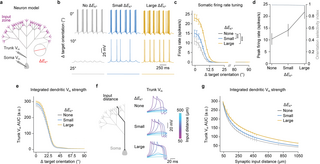
Our data suggests that the local [K⁺]_o increases in dendritic segments receiving similarly tuned inputs can boost the reliability and duration of dendritic spikes without compromising feature selectivity (Fig 2g and 2h). Thus, we next sought to investigate the functional consequences this result might have on the somatic neuronal output. For this, we constructed an abstract neuron model using a fractal tree, mimicking the generic compartmentalization and fractal dimensionality of the apical dendritic tree of pyramidal neurons [75,76] and we stimulated distal dendrites with similarly tuned input [38,77,78] (Fig 4a). We simulated 3 conditions of E_K⁺ shifts in the stimulated dendrites: no change, small shift, or large shift, based on the [K⁺]_o changes determined in Fig 1 (Fig 4a and 4b; see Methods). These 3 levels correspond to ΔE_K⁺ = 0 mV, ΔE_K⁺ = 6 mV, and ΔE_K⁺ = 18 mV, respectively, to represent the case of no contribution as well as the minimum and maximum level used in (Fig 1), based on in vivo recordings. In S6 Fig, we also included a similar test using a reconstructed neuron morphology based on a previously published model.

Fig 4. Local dendritic E_K⁺ shifts induces neuronal firing gain modulation.

(a) Diagram of the abstract neuron model. The neuron received orientation-tuned synaptic input at the distal dendrites and local E_K⁺ shifts. (b) Example soma V_m traces obtained as a function of dendritic E_K⁺ shift magnitude and stimulus orientation relative to target orientation. (c) Soma firing rate tuning curve for different dendritic E_K⁺ shift magnitudes. Error bars are mean ± SEM. (N = 15 simulations). ***P = 10⁻¹⁶ and 10⁻³⁰ for small and large E_K⁺ shifts, respectively, one-tailed Student’s t test. (d) Soma peak firing rate at target orientation and orientation selectivity index as a function of dendritic E_K⁺ shift magnitude. Error bars are mean ± SEM. (N = 15 simulations). (e) Area under the curve for the dendritic trunk V_m measurements as a function of stimulus orientation relative to target orientation and dendritic E_K⁺ shift magnitude. Error bars are mean ± SEM. (N = 15 simulations). Trunk length was kept constant at 500 μm. Note that bAPs were here abolished by silencing voltage-gated sodium channels in the trunk and soma. (f) Example dendritic trunk V_m traces obtained at the target orientation as a function of synaptic input distance to soma and dendritic E_K⁺ shift magnitude. (g) Area under the curve for the dendritic trunk V_m measurements at the target orientation as a function of synaptic input distance to soma and E_K⁺ shift magnitude. Error bars are mean ± SEM. (N = 15 simulations) and solid lines represent fit to the function f(x) = x^a+c. ***P = 0.61, 0.41, and 0.38 for different E_K⁺ shifts. See also S7 Fig and S2 Table.

https://doi.org/10.1371/journal.pbio.3002935.g004

These simulations revealed that somatic firing rates were significantly amplified when E_K⁺ values were shifted locally (Fig 4c and 4d; P = 0.007 and P = 0.003 for small and large E_K⁺ shifts, respectively, one-tailed Student’s t test, N = 15 simulations). We determined that this form of gain modulation was consistent with a multiplicative transformation (S7 Fig; gain coefficient = 1.64 and 2.73 for small and large E_K⁺ shifts, respectively), similarly to previously shown in the visual cortex [79]. This amplification was similar to the one expected by increasing the number of synapses (S8 Fig) with the main difference being that E_K⁺ modulation closely follows the dendritic activity levels, operating in time scales of seconds. Importantly, and in congruence with what we observed in the dendrites (Fig 2h), the somatic firing selectivity was not changed by E_K⁺ shifts despite increases in firing rate also for orientations away from the target orientation (Fig 4c and 4d; orientation selectivity index: 0.99, 0.98, and 0.98 for no, small, and large E_K⁺ shifts, respectively; N = 15 simulations). To elucidate how dendritic E_K⁺ shifts cause dendritic gain modulation, we measured the area under the curve of the integrated V_m signal arriving at the base of the dendritic trunk during a stimulation event. To exclude back-propagating action potentials (bAPs), for this analysis, we turned off the voltage-gated sodium channels in the soma and trunk. This showed that the strength of the integrated dendritic signal, received by the soma, rose substantially with increasing E_K⁺ shifts (Fig 4e); for example, the signal strength at the target orientation increased by around 12% when imposing large E_K⁺ shifts compared to no E_K⁺ shifts.

Finally, we asked what functional benefits there might be to this K⁺-mediated gain modulation. A major task of dendrites is to transmit incoming inputs to the soma for output generation. This is an inherent challenge, especially for distal inputs to large neurons, as the voltage signal tends to attenuate as a function of distance traveled and branching points [80,81]. We, therefore, speculated that one function of K⁺-mediated gain modulation might be to promote neurons transmitting signals over larger dendritic distances. To test this, we manipulated the synaptic input distance to the soma by scaling the entire neuron while measuring the integrated V_m signal at the base of the neuron (Fig 4f and 4g). Interestingly, due to the local gain of the synaptic input, the E_K⁺-shifted regime is attenuated less with distance. This, in turn, makes it possible for signals to travel substantially longer, before reaching a similar integrated V_m signal. Based on the power-law fits using the χ² fitting method for each ΔE_K⁺ condition, we observe that as the neuron grows, the signal in the absence of E_K⁺ shift is attenuated by a factor when compared to the large E_K⁺ shifts (Fig 4g). Together, these results show that local activity-dependent [K⁺]_o increases and E_K⁺ shifts in dendrites enhance the effectiveness of distal synaptic inputs to cause feature-tuned firing of neurons, without comprising feature selectivity.

We defined a dendritic segment as a cylinder with length L = 10 μm and radius R₁ = 1 μm [32,45–47]. Each segment was randomly populated with 7 to 13 synapses, yielding synaptic densities comparable to that of neocortical neurons [51–53]. The orientation preference of individual synapses of a dendritic segment depended on the synaptic organization type to which the segment belonged, that is, the diverse or similar input tuning regime. Synapses in segments with similar tuning were assigned an orientation preference using a half-circular normal distribution with σ = 15° [42,72,108] and a mean target orientation arbitrarily set to 0°, while synapses in segments with diverse tuning were assigned orientation preferences using the uniform distribution. Importantly, for both types of input regimes, we could reproduce the synaptic orientation preference cumulative distributions measured previously in the visual cortex of ferrets [42]. Moreover, the orientation preferences of our diverse tuning regime resembled those previously recorded in the visual cortex of mice [45,54]. All synapses, irrespective of the spatial organization regime, had a tuning curve width given by a half-circular normal distribution with σ_tuning = 11° [42,55], and the activity of each synapse spanned from 0 to 1 (Fig 1c). This sampling method for the number and tuning properties of excitatory synapses of dendritic segments was implemented throughout this work.

We modeled the activation of synapses of dendritic segments by assuming that all synapses were activated by visual stimulation according to their tuning curve. To assess the expected synaptic activity level of a segment for a given stimulus orientation, we calculated the average activity of all synapses in that segment, w(θ), that depends on the orientation tuning of each synapse and the distribution of orientation preferences in the dendritic segment (Fig 1d and 1e). We then obtained the synaptic activity factor by comparing the expectation values from the synaptic activity distributions for the 2 types of dendritic segments. We sampled 10⁴ dendritic segments and used a Gaussian kernel density estimator to determine the probability density function p(x) for the expected synaptic activity distributions for each segment type. The expectation value was calculated as E(X) = ∑_ix_ip_i where x was a linearly spaced set of values between 0 and 1. To investigate the stimulus orientation-dependent modulation of the synaptic activity factor (Fig 1f), we repeated this procedure for all stimulus orientations in the interval θ ∈ [0: 90°].

The exact size and shape of the extracellular space surrounding functionally mapped, short dendritic segments is currently unknown, so we chose to model it as a cylinder that encapsulates the dendritic segment cylinder. The space in between these 2 cylinders thus constitutes the extracellular space in our investigations, and its volume (V_ext) is given by:
(4)

With R₁ and R₂ being the radius of the inner and outer cylinder, respectively, both with length L = 10 μm. This can be rewritten to express the volume ratio (V_R) as the ratio between the 2 cylinders:
(5)

During synaptic excitatory transmission, K⁺ ions are released into the extracellular space primarily through NMDA receptors [16,21,26,27] and move around due to diffusion, although their movement is hindered by various cellular elements within the extracellular space. To account for this hindrance, we define effective diffusion as a function of tortuosity [66]:
(6)

Here, is the diffusion of free K⁺ ions in physiological saline, λ is a non-dimensional measure of how hindered an ion is in its movement in a given space, and D* is the resulting diffusion rate. The parameter for and λ were based on previous work [57,66,109,110]. Here, we assume that diffusion in the radial direction is negligible, as the extracellular space is very small compared to the dendritic segment length. Moreover, we assume closed boundary conditions on the outer cylinder wall, since the extracellular space mainly contacts cellular membranes of neighboring neurons and/or glial cells. Finally, assuming the extracellular K⁺ behaves like a brownian particle, the spatial diffusion of the K⁺ will extent as a multivariate normal distribution with standard deviation [111,112]. This equates the average distance traveled for an individual particle, after a certain characteristic time τ. Using this equation, we can likewise compute the time it will take for a particle to diffuse at a distance L:
(7)

After this characteristic time τ, we assume that the [K⁺]_o is well-mixed and uniform throughout the extracellular space. For the dendritic segment with length L = 10 μm, the characteristic time becomes τ ≈ 66 ms. Considering that the majority of K⁺ efflux occurs within ≈ 100 ms from initial synaptic activation, we predict a peak [K⁺]_o elevation along the dendritic segment after ~150–170 ms, for a τ ≈ 66 ms. Following, pumps and channels return the K⁺ levels to baseline, yet operating on much lower timescales as seen in in vitro experiments [58,59] (see S2 Text and S9–S13 and S15 Figs for simulations that describe the spatial and temporal properties of K⁺ diffusion in the presence of Na⁺/K⁺ pumps). Thus, we analyzed our models with fixed [K⁺]_o changes, with values chosen as described in the section below. This time scale separation, due to the different time constants of the described phenomena, has been successfully applied previously on similar questions [113]. Finally, we assume that the boundary between the dendritic segments is closed, implying a finite ion concentration within the segment. This limits our approach since we do not investigate the effect of spillover K⁺ ions moving along the dendrite, potentially affecting neighboring segments. However, given the average distance traveled for a K⁺ ion between the stimuli considered here (based on Eq 7, the expected movement is ≈ 30 μm during a period of 600 ms), only the directly neighboring segments could potentially be affected, thus keeping the ionic shift highly localized (S10 Fig).

To estimate synaptic activity-dependent [K⁺]_o changes near dendritic segments, we assumed that local increases in [K⁺]_o are linearly correlated with the expected synapse activity, as a result of K⁺ efflux from the intracellular space. By scaling the K⁺ change in the diversely tuned input regime with the stimulus orientation-dependent synaptic activity factor, we obtained an estimate of the K⁺ change in the similarly tuned regime. Using this, in conjunction with Eq 5, we derived equations for the 2 types of input regimes:
(8)
(9)

With Δ[K⁺]_o and Δ[K⁺]_i being the change in extracellular or intracellular [K⁺], respectively, V_R the volume ratio as defined in 5 and E(θ) being the stimulus orientation-dependent synaptic activity factor. Using the Nernst equation, we then can express the shift in E_K⁺ (see Eq 2).

We simulated the dendritic segment V_m as an isolated resistance-capacitance circuit, similar to the common practice for point-neuron models [70]. The major differences between point-neuron models and the point-dendrite model developed here stem from the specific ion channel setup and cellular resistance, chosen to mimic dendritic properties [73] (S1 Table). The circuit is given by the ordinary differential equation:
(10)

C_m Is the membrane capacitance, set to 2 to simulate the contribution from the spines [114], I_ext is the current generated by synaptic receptors (AMPA and NMDA receptors), and I_int is the current generated by intrinsic ion channels (K_leak, Na_V, K_V, K_M, K_A, K_Ca, C_aV, and HCN). The latter is multiplied by the surface area, A, as these channels are scattered uniformly along the surface of the dendrite. All relevant channel dynamics and specific parameters are included in the S1 Text. The system was simulated using an exponential Euler scheme (cnexp):
(11)

Here, V_∞ is the solution to the equation :
(12)
Where denotes a channel’s average conductance, n^x is from the individual channel dynamics controlling the gating and channel-specific conductance, E_ion denotes the relevant reversal potential and sums the current from the different types of synaptic receptors, were . For complete synaptic equations for NMPA, NMDA, and GABA_A receptors, see S1 Text. The membrane time constant is given as follows:
(13)

The point-dendrite model was populated with orientation-tuned synapses as described in the previous section. The orientation-tuned synaptic activity in the point dendrite was implemented by multiplying g_AMPA and g_NMDA of synapses with the average synaptic activity, w(θ), that depends on the orientation tuning of each synapse and the distribution of orientation preferences in the dendritic segment, according to Fig 1d and 1e. For each stimulation presynaptic event, all synapses were activated with a Poisson distributed delay (λ = 80 ms). The orientation tuning of the individual synapses was achieved by scaling the AMPA and NMDA conductance according to the synapse’s tuning curve given by a half-circular normal distribution with σ_tuning = 11° (see Fig 1c) [42,55,72,108]. To create a stimulation train consisting of several input events, we replicated the synaptic activation 2 times with a constant delay of 300 ms in between events. Based on our analysis in the Methods section “K⁺ diffusion state,” the S2 Text, and the S9–S13 Figs, we modeled the activity-dependent local increase in [K⁺]_o a step function in between events: The first stimulation event was regarded as the control condition with ΔE_K⁺ = 0 mV, and the 2 subsequent events as the experimental condition for a given E_K⁺ shift in the interval ΔE_K⁺ ∈ [6:18 mV]. We used a V_m of –30 mV as a threshold criterion for identifying dendritic spikes. This value was chosen because we observed the largest change in V_m around this value, as synaptic integration transitions from subthreshold input summation to suprathreshold spiking. To evaluate the effect of nonspecific inhibitory (GABA_A) input, we repeated our point-dendrite model simulations in the presence of inhibition. Specifically, we simulated the activation of GABA_A synapses randomly activated at 10 Hz (S2 Fig).

To investigate the relationship between the average synaptic activity, w(θ), (Fig 1e), the ΔE_K⁺, and the number of synapses (N) for the emergence of a dendritic spike, we independently varied each variable in small increments in the point-dendrite model. By doing so, we identified the lowest value of ΔE_K⁺ that was able to push the V_m over the threshold of –30 mV, our working criterion for dendritic spike generation, given N and w. We assumed that the relation between the 3 parameters was linear, and we, therefore, fitted a plane to obtain a model of ΔE_K⁺ needed to trigger dendritic spikes as a function of N and w. For this, we used the planar equation αw + βN + ν = 0 and solved it as Ax = b (S3 and S4 Figs and Table 1 for coefficients):
(14)

From this equation, we can see that adding 1 additional synapse would lower the required ΔE_K⁺ for a dendritic spike by 2.08 mV. Accordingly, a 10% increase in w would lower the required ΔE_K⁺ for a dendritic spike by 3.8 mV. Note that in this work w varies between 0 and 1 and the maximum number of synapses on a dendritic segment is 13 [51–53]. A combination of sufficiently high number of synapses N and w would lead to negative ΔE_K⁺, in which case we assumed to correspond to no E_K⁺ shift. From this, we could then estimate the dendritic spike probability as a function of ΔE_K⁺ and stimulus orientation. Using statistical formalism for the setup of the dendritic segments with similarly tuned inputs, we sampled the number of synapses and synaptic orientation preferences of 10⁴ segments, and calculated the average synaptic activity, w(θ). Following, we determined the ΔE_K⁺ needed to generate a dendritic spike according to ΔE_K⁺ (N, w) = αN + βw + ν for each stimulus orientation. For a stimulus presented in the target orientation, we compared this value with a set of ΔE_K⁺ values in [0, 6, 10, 18 mV] to determine whether each sampled segment fired a dendritic spike or not. To obtain the set ΔE_K⁺ values for the other orientations, we multiplied the set ΔE_K⁺ values of the target orientation with the normalized version of the synaptic activity factor seen in Fig 1f and repeated the comparison with the respective needed ΔE_K⁺ value. Finally, we calculated the fraction of dendritic segments, at each orientation, that would be expected to show dendritic spikes and converted this into a probability.

To understand the biophysical principles governing the regulation of dendritic spikes by local K⁺ changes, we used dynamical systems theory [74]. While our point-dendrite model is defined by the differential Eq 10, it is not possible to solve it analytically. Rather, we chose to plot the exact solutions to the differential equations evaluated at different V_m as a vector plot, which in essence is similar to summing all I-V curves from the included intrinsic and synaptic channels. We thus have V_m on the first axis, and on the second we have its derivative which in our case is denoted . The time evolution of the synaptic currents in the point dendrite model was described as before (see S1 Text). Synaptic receptors were simulated in the time interval [0: 100 ms] using the Euler method. For each time step, an I-V curve was generated and the resulting I-V curves were concatenated to create a time-dependent I-V landscape (Fig 3e and S1 Video). To compare the effect of [K⁺]_o changes, we simulated the system with ΔE_K⁺ = 0 mV and ΔE_K⁺ = 18 mV.

Using the NEURON simulation environment, we constructed an abstract neuron model to systematically test the role of local [K⁺]_o elevations on dendritic input integration and somatic output firing. The dendrite’s morphology was constructed as a fractal tree (Fig 4a): for each dendritic section generation, 3 new sections, each with half the length of the former, were added (length of the most distant section: 20 μm). This gave a fractal with dimension D = ln 3/ ln 2 = 1.58, mimicking the generic compartmentalization and fractal dimensionality of the apical tree of pyramidal neurons [75,76]. The fractal dendritic tree was extended with a trunk dendritic compartment (500 μm) and a soma (length 30 μm, diameter 10 μm) to complete the neuron morphology, and intrinsic ion channels (K_leak, Na_P, Na_T, K_P, K_T, K_DR, K_Ca, KM, Ca_LVA, Ca_HVA, and HCN) were inserted into the cellular compartments (S2 Table), based on [73]. Using this morphology enabled us to test the effect without hidden edge cases caused by morphology, as regardless of the placement of the cluster the effect should remain the same. The fractal dimension kept the properties of the neuron as close as possible to that of a detailed morphology.

To investigate the compartmentalization of dendritic integration under the different ΔE_K⁺ values, we stimulated synapses residing in segments with similar orientation tuning on the most distant dendritic branches [38,77,78]. For this, a Poisson-distributed number of dendritic segments (λ = 32 segments) were selected to host the similarly tuned inputs in each simulation iteration, and the number of synapses and their orientation tuning were sampled as described above. Only distal dendrites received direct input, to ensure a constant distance to the soma. The local ΔE_K⁺ of stimulated dendrites were grouped into 3 conditions: no shift (ΔE_K⁺ = 0 mV), small shifts (ΔE_K⁺ = 6 mV), or large shifts (ΔE_K⁺ = 18 mV), based on the [K⁺]_o changes found in Fig 1. As before, the orientation tuning of individual synapses was achieved by scaling the AMPA and NMDA conductance. To simulate a realistic somatic firing pattern, the synapses within each dendritic segment were activated randomly given by a Poisson distribution with λ = 30 ms. This stimulation protocol was repeated 3 times with a 300 ms delay between stimulation events. Each neuron setup was simulated with each of the 3 ΔE_K⁺ conditions to directly assess the effect of the local K⁺ changes.

In this investigation, we only considered the activity-induced changes of [K⁺]_o and assumed the concentration of all other ions to remain constant. We assume contributions from Na⁺ and Ca²⁺ to be minimal and their effects covered within the range of the E_K⁺ demonstrated. This difference in the respective contributions arises from the ratio between the intra and extracellular volume, where the former is assumed to be at least a factor of 2 larger [62–64] (the size of the extracellular space ranges from 0.04 to 0.5 μm [63,104]), and is smaller than the pyramidal neuron dendritic diameter [105,106] and is also motivated by our previous experimental recordings documenting in vivo elevation of [K⁺]_o [14]. This results in greater changes seen in the extracellular space, and combined with the formulation of the Nernst equation, the shift in E_K⁺ outweighs the other ions. For a more in-depth discussion about this, see S3 Text and S14 Fig.

We assumed that the gain modulation of the somatic firing tuning curve could be described by a multiplicative or additive function, similar to previously described in the visual cortex of mice [79]. The multiplicative and additive functions are given by:
(15)
(16)

Here, FR_Before(θ) and FR_After(θ) are the somatic firing rates at a given orientation with non-shifted or shifted E_K⁺ values, respectively, ξ is the fit parameter that describes the change in firing rate either as a gain coefficient or as a gain constant for the multiplicative and additive gain transformation, respectively. To determine the fit parameters, we fitted the 2 functions to the firing rate tuning curve data using the χ² fitting method (Table 2 and S7 Fig). Only the multiplicative method was able to produce a satisfying fit and capture the main features of the tuning curve, whereas the additive only captured the responses to orientations close to the target orientation.

Table 2. Fitted gain parameters.

Gain parameters obtained for the multiplicative (top) and additive functions (bottom) for the small and large E_K⁺ shifts (left and right, respectively). Errors were assumed Gaussian and reported as standard deviations. See also S7 Fig.

https://doi.org/10.1371/journal.pbio.3002935.t002

The orientation selectivity index was computed as 1 –circular variance (CV) in orientation space given by:
(17)
Where r_k is a measurable output at orientation θ_k (in radians); here, we used dendritic spiking probability and somatic firing rate as output measures. To compute OSI, we mirrored the results obtained in the simulation between [0:90°] to obtain values in the interval [−90:90°].